For data analyst freelance services contact me [email protected]
“How long do customers surf on the new panel we built for them, on average?” asked the CTO of the company I worked for. “It doesn’t matter what the average of all customers is,” I replied, “the average usually lies and insights cannot be inferred from it. If you really want to understand how your customers behave, you should examine the distribution of their browsing duration, and if you want to dig deeper, it’s worth looking at the box-plot chart as well, so we can get a broader picture.”
In my response, I may have slightly minimized my attitude towards the average. Sometimes there is room to look at the average when analyzing a customer population, but a data analyst can only draw insights from the average when the customer population is homogenous, which is not usually the case.
Example of the idea that the average function can lie
To demonstrate the idea, let’s look at loan request data from Landing Club customers between 2007 and 2015. (Landing Club is a fintech company that specializes in peer-to-peer loans, and the data was published on Kaggle.)
During this time period, there were 887,000 loan requests, with an average request amount of $14,755. But does this number mean that most requests are around $14,755? The answer is no! The average tells us very little about the nature of the requests and can even be misleading.
When looking at the distribution of requests using a histogram graph, we can see that the total amount of requests is not distributed homogeneously and therefore we cannot draw conclusions about the loans that customers are requesting based solely on the average.
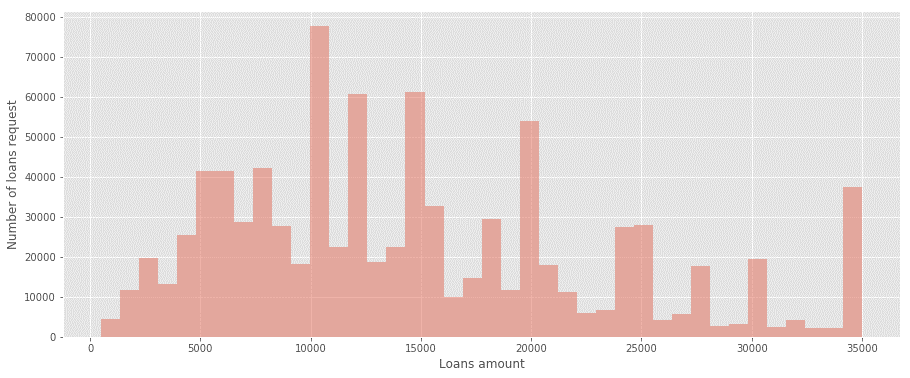
According to the histogram, we can see that there are many customers who request loans in low amounts that pull the average down, while there is also a large group of customers who request loans totaling $35,000 and above that pull the average up.
Another way to examine the data is with a box plot, which can easily show us where 50% of the customers are concentrated.
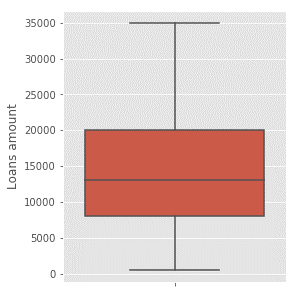
The red box shows that 50% of loan requests are for amounts between $8,000 and $20,000. The lines next to the box represent the population distribution, and as with a histogram, we can see that the loan amounts are highly heterogeneous and not concentrated around a single point.
By the way, the line in the middle of the box is the median, which stands at $13,000. The median is not affected by extreme values, so loan requests from customers at the distribution ends have less impact on it. However, like the mean, it also does not help us describe the heterogeneous population.
Relying solely on the mean, without the help of other variables, may obscure interesting insights that appear in the data. In the data published by Landing Club, customers are classified according to their risk level. The risk level for financial customers describes the probability that the customer will repay the loan and not default. Risk level ‘A’ refers to non-risky customers and ‘G’ refers to the riskiest customers.
Breakdown by segments
When segmenting the loan requests by the variable of risk level, one can see the strong correlation between the customer’s riskiness and the average loan request amount. The more risky the customer is, the more they tend to request a larger loan.
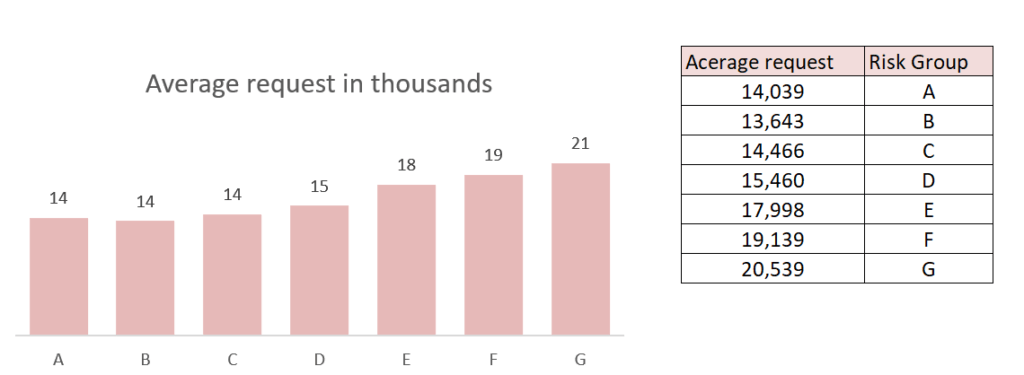
The relationship we found can also be illustrated using a box plot:
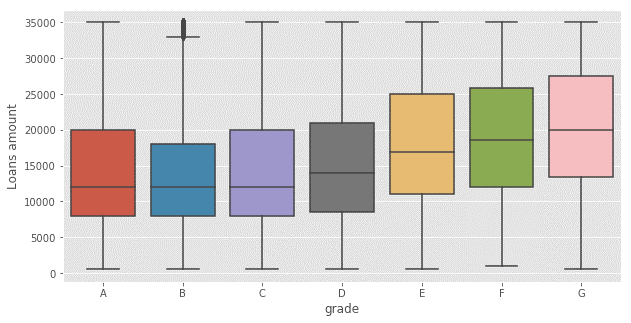
The chart also shows how the loan requests are distributed for each risk level.
To summarize
It is always advisable to suspect that the mean is deceiving and causing us to draw incorrect conclusions about the population. If we still choose to work with the mean, it is advisable to check the homogeneity of the population using dispersion measures such as variance and standard deviation.
The recommended way to draw conclusions about a heterogeneous population is by using graphs such as histograms and box-plots.
Relying solely on the mean may conceal additional insights that are hidden in the data and can only be revealed when analyzed using additional customer characteristics.
If you want to analyse your data you may contact me at: [email protected]
You may also hire me through upwork platform on that link:
https://www.upwork.com/freelancers/~018940225ce48244f0\





