לחברות המעוניינות בשירותי פרילנס או סדנאות של אנליסט, ניתן לפנות אליי [email protected]
**** לפודקאסט של הבלוג לחצו כאן ****
הקדמה
זהו החלק השלישי במדריך לניתוח נתונים בשפת פייתון ל- דאטה אנליסט.
חלקים נוספים של המדריך:
- ניתוח נתונים בשפת פייתון – חלק א.
- ניתוח נתונים בשפת פייתון – חלק ב.
- התקנת סביבת העבודה של פייתון בחינם.
בחלקים הקודמים של המדריך עסקתי בהיבטים של ניתוח נתונים בעזרת השפה.
כפי שציינתי בחלקים הקודמים, ההמלצה שלי היא להשתמש בשפת SQL עבור אנליזות וניתוחי נתונים כיוון ששפת פייתון היא במהותה שפת תכנות שלא נועדה לניתוח נתונים ולכן ניתוח נתונים בפייתון היא עבודה מסורבלת הגוזלת מה- דאטה אנליסט זמן יקר על פעולות שהוא יכול לבצע בקלות בשפת SQL.
יחד עם זאת ישנם ניתוחים סטטיסטיים מתקדמים שלא ניתן לבצע בשפת SQL ובמדריך זה אראה כיצד ניתן לבצע ניתוחים אלו בשפת בפייתון.
שימו לב, המדריך נכתב עבור דאטה אנליסט ולא עבור דאטה סיינטיסט ולכן התמקדתי במדריך זה בסקירה של כלים סטטיסטיים המאפשרים לקבל תובנות מנתונים ולא בשיטות לבניית מודלי ניבוי.
מסיבה זאת גם העדפתי להשתמש בחבילת statsmodels על מנת ליצור מודלים סטטיסטיים ולא בחבילת scikit-learn הפופולרית. התוצרים (פלטים) של חבילת statsmodels עשירים יותר במידע סטטיסטי שיכול לעזור בהפקת תובנות על הנתונים.
המדריך נכתב בלשון זכר אך מתאים לכל המינים.
יבוא של ספריות והכנת טבלאות
החבילות העיקריות שנעבוד עליהם במדריך הם statsmodels ו scipy ו Pandas.
בשלב הראשון, לפני הניתוחים הסטטיסטיים אני מיבא את החבילות והטבלה שנעבוד עליה ומבצע מניפולציה על המשתנים כדי שיהיה קל יותר לנתח אותם.
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
import statsmodels.stats.descriptivestats as smd
import pandas as pd
from scipy import stats
pd.set_option('display.float_format', '{:.2f}'.format)
houses = pd.DataFrame(sm.datasets.get_rdataset("HousePrices","AER").data)
houses.driveway.replace(('yes', 'no'), (1, 0), inplace=True)
houses.recreation.replace(('yes', 'no'), (1, 0), inplace=True)
houses.fullbase.replace(('yes', 'no'), (1, 0), inplace=True)
houses.gasheat.replace(('yes', 'no'), (1, 0), inplace=True)
houses.aircon.replace(('yes', 'no'), (1, 0), inplace=True)
houses.prefer.replace(('yes', 'no'), (1, 0), inplace=True)
houses.head(5)
הערות:
- בתוך החבילה של statsmodels ישנן טבלאות רבות שאפשר להתאמן עליהן (לרשימת הטבלאות לחץ כאן).
- בדוגמאות הבאות אעבוד בעיקר עם טבלה בשם HousePrices המתארת את מחירי הבתים בעיר וינדזור בקנדה.
- בטבלה ישנם משתנים בוליאנים עם ערכים של Yes ו No ובעזרת replace אני ממיר אותם ל 1 ו 0 על מנת להקל בחישובים הסטטיסטים שאבצע בהמשך.
סטטיסטיקה תיאורית עם statsmodels
לחבילת statsmodels יש פונקציות של סטטיסטיקה תיאורית שלה מדדים סטטיסטיים רבים שכדאי להשתמש בהם כאשר לומדים על טבלאות חדשות:
a=smd.describe(houses)
pd.DataFrame(a)
ביצוע מבחן T-test בפייתון עם scipy
מבחן T בודק האם ההבדל בין הממוצעים של שתי קבוצות הוא מובהק. להרחבה על התאוריה של מבחני T והשוואה בין תוחלות לחצו כאן.
בפייתון ניתן לבצע את מבחן T בעזרת החבילה של scipy שבה יש מבחני מובהקות מסוגים שונים.
בדוגמה הבאה נריץ את מבחן T כדי לבדוק האם מחירי הדירות שיש בהם מזגן יקרות יותר באופן מובהק.
price_with_aircon = houses.query('aircon == 1')['price']
price_without_aircon = houses.query('aircon == 0')['price']
a=houses.groupby('aircon').describe()['price']
print(a)
a = stats.ttest_ind(price_with_aircon, price_without_aircon, alternative='greater')
print("p-value: "+format(a.pvalue,',.2f'))
print("tstat: "+format(a.statistic,',.2f'))
ונקבל את הפלט:
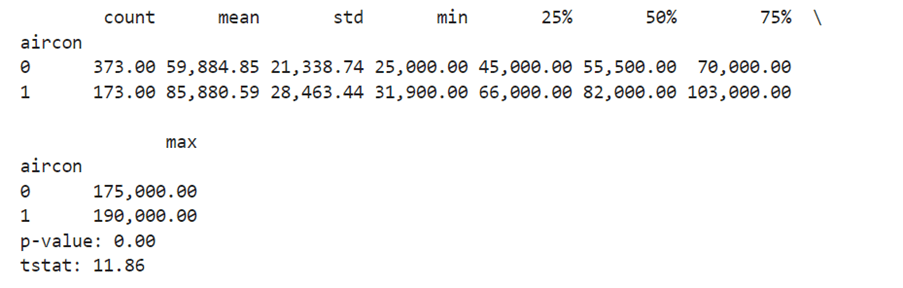
הסבר לתוצאות מבחן T
הממוצע של דירות ללא מזגן הוא 59,884 דולר ודירות עם מזגן הוא 85,880 דולר.
לפי מבחן T ההבדל בין הממוצעים הוא הבדל מובהק כיוון שה- p-value קטן 0.05.
שימו לב:
במבחן לא התייחסתי לנושא של הנחות. בסעיפים הבאים אפרט על מבחנים שיכולים לעזור לתקף את ההנחות של מבחני T.
בדיקת שפירו-וליקס בעזרת פייתון
בעזרת מבחן שפירו-וילקס ניתן לבחון האם האוכלוסייה מתפלגת נורמלית.
בעזרת חבילת scipy נוכל לבצע כך את המבחן:
from scipy import stats
print(stats.shapiro(price_with_garage))
print(stats.shapiro(price_without_garage))
שימו לב שכשאר תוצאות מבחן שפירו מראות על מובהקות המשמעות היא שהשדה אינו מתפלג נורמלית וזה אומר שעלולה להיות בעיה להשתמש במבחן T כאשר מספר התצפיות נמוך.
בדיקת שונויות בעזרת פייתון
גם את מבחן לוין הבודק שונויות ניתן לבצע בעזרת חבילת scipy:
a=stats.levene(price_with_aircon, price_without_aircon)
print(format(a.pvalue,',.2f'))
שימו לב שכשאר תוצאות מבחן לוין מראות על מובהקות זה אומר שהשוניות אינן זהות ועלולה להיות בעיה להשתמש במבחן T.
מבחן Mann-whitney עם פייתון
במקרה והנתונים אינם עונים על הנחות היסוד של מבחן T ניתן לבצע מבחן Mann-whitney במקום מבחן T להרחבה על מבחן Mann-whitney לחצו כאן.
את מבחן Mann-whitney נוכל גם לבצע בעזרת חבילת scipy באופן הבא:
a=stats.mannwhitneyu(price_with_aircon, price_without_aircon)
print(format(a.pvalue,',.2f'))
– פרסומת –
**** לפודקאסט של הבלוג לחצו כאן ****
בניית רגרסיה ליניארית בשפת פייתון בעזרת statsmodels
בעזרת רגרסיה לינארית ניתן לנבא ערכים כמותיים ולהעריך מה המשתנים שהכי משפעים על המשתנה הנבדק. להרחבה על בניית רגרסיה לינארית לחצו כאן.
בדוגמה הבאה אעזר ברגרסיה לינארית בכדי לאתר מה הם המשתנים שמשפעים על מחירי הדיור בטבלה שעבדנו עליה בסעיפים הקודמים.
שימו לב, לפני הרצת רגרסיה לינארית יש לוודא שהנתונים עומדים בהנחות היסוד של המודל כלומר, אין מולטיקולינאריות בין המשתנים והקשר בין המשתנים למשתנה התלוי הוא לינארי.
יצירת רגרסיה לינארית ב- statsmodels
הקטע קוד הבא מריץ רגרסיה לינארית בעזרת חבילת statsmodels
results = smf.ols('price ~ lotsize+bedrooms+bathrooms+stories+driveway+recreation+fullbase+gasheat+aircon+garage+prefer', data=houses).fit()
print(results.summary())
הסבר
- הפונקציה OLS של חבילת stasmodels מחשבת את הרגרסיה הלינארית.
- המשתנה price הוא המשתנה התלוי וכל שאר המשתנים לאחר הסימון ~ שמחוברים ב + הם המשתנים הבלתי תלויים.
פירוש התוצאות רגרסיה לינארית ב- statsmodel
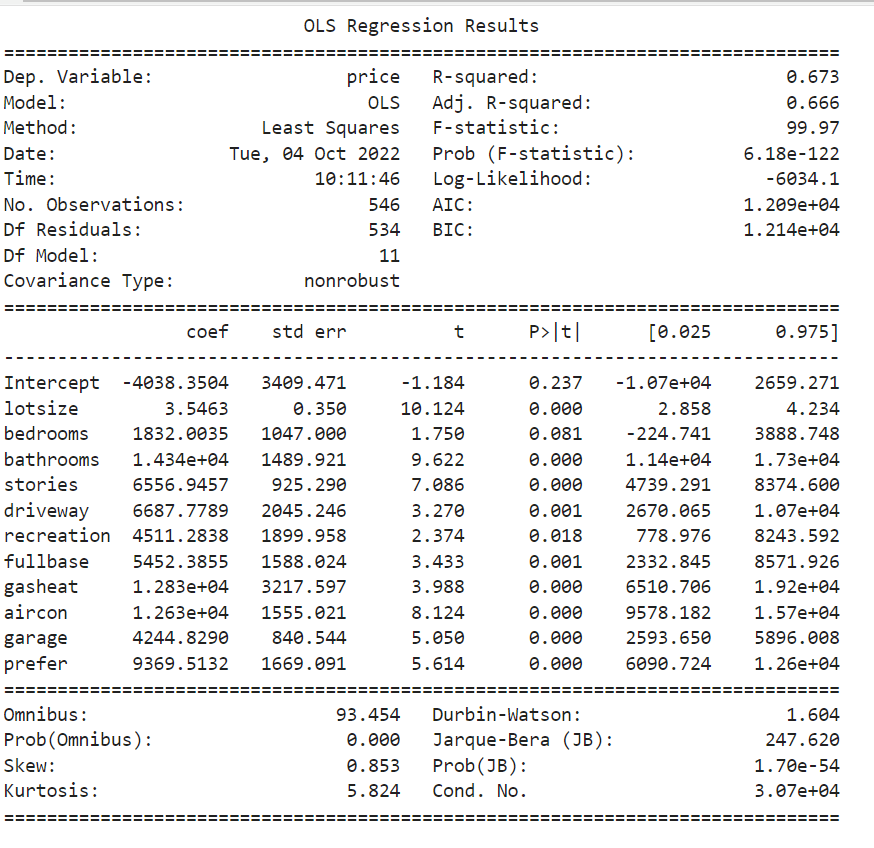
מהתוצאה אנחנו יכולים לראות שהרגרסיה מסבירה בצורה טובה את השונות של המשתנה התלוי (מחירי הדירות) כיוון שהתוצאה של R-Squared היא יחסית גבוהה (0.673).
העמודה P>|t| מראה את המובהקות של כל המשתנים ברגרסיה. אם המשתנים לא מובהקים יש להריץ את הרגרסיה מחדש ולהסיר את המשתנים הלא מובהקים.
ביצוע פעולת standardized betas ברגרסיה לינארית בשפת פייתון
השפעת המשתנים הבלתי תלויים על המשתנה התלוי הינה בסקאלה של מבחני T. אך יש לנו אפשרות גם לראות את ההשפעה של כל משתנה על המודל גם לפי סקאלה אחרת. שיטה זאת מכונה גם – standardized betas.
להלן דוגמה לנרמול משתנים והרצה של הרגרסיה הלינארית:
houses_z_scaled = houses.copy()
# apply z score normalization
for column in houses_z_scaled.columns:
houses_z_scaled[column] = (houses_z_scaled[column] –
houses_z_scaled[column].mean()) / houses_z_scaled[column].std()
results = smf.ols('price ~ lotsize+bedrooms+bathrooms+stories+driveway+recreation+fullbase+gasheat+aircon+garage+prefer', data=houses_z_scaled).fit()
pd.DataFrame(results.params).sort_values(0,ascending=False)
התוצאה של הרגרסיה תהיה זהה לרגרסיה הקודמת שהרצנו אך המשתנים התלויים בה מנורמלים לאותה הסקאלה וכך ניתן להשוות בניהם בקלות:
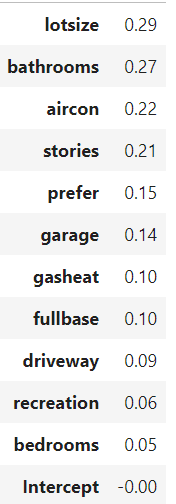
בניה של רגרסיה לוגיסטית בפייתון עם statsmodels
רגרסיה לוגיסטית משמשת לניבוי של תופעות בינריות (1 או 0). כלומר בעזרת הרגרסיה אנחנו יכולים לנבא האם תופעה תתרחש או לא. הרגרסיה הלוגיסטית גם יכולה להראות לנו את ההשפעה של כל אחד מהמשתנים המסבירים על התופעה שהרגרסיה מנסה לנבא. ההשפעה של משתני הרגרסיה על המשתנה התלוי יכולה לעזור לנו להבין לעומק מה הסיפור שמסתתר מאחורי הנתונים.
בדוגמה הבאה נעזר בטבלת מחירי הדיור שעבדנו איתה בסעיפים הקודמים אך הפעם ננסה להסביר מה הגורמים שמשפיעים על כך שבדירה יהיה מותקן מזגן.
הרצת הרגרסיה הלוגיסטית
בשביל הרצת הרגרסיה נריץ את השורות הבאות:
results_logit = smf.logit('aircon ~ price+lotsize+bedrooms+bathrooms+stories+driveway+recreation+fullbase+garage+prefer+gasheat', data=houses).fit()
print(results_logit.summary())
פירוש התוצאות של רגרסיה לוגיסטית ב- statsmodels
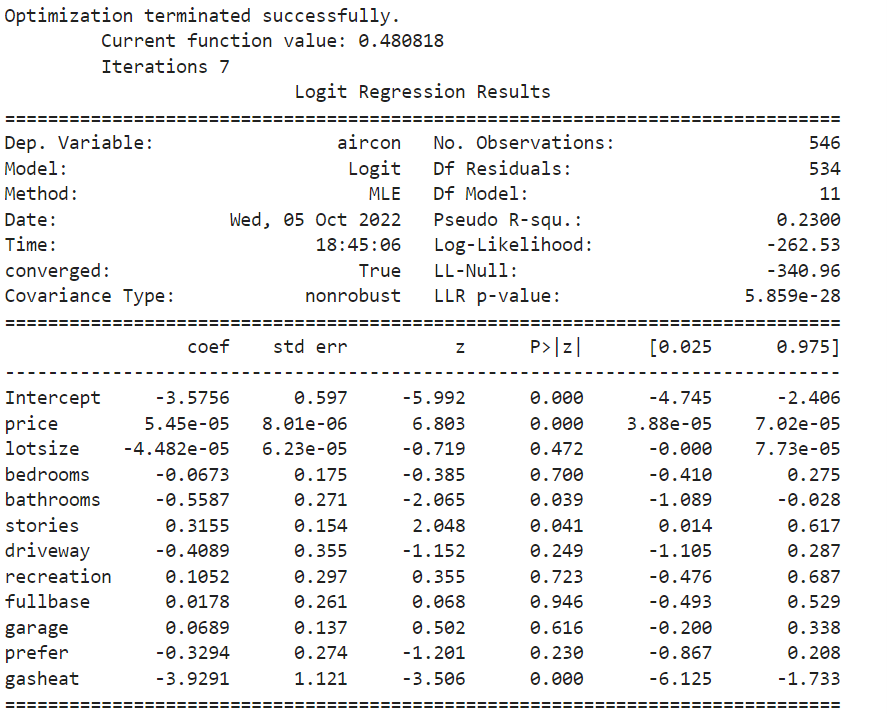
בעמודה |P>|Z אנחנו יכולים לראות עד כמה מובהק כל אחד מהמשתנים במודל.
אנחנו יכולים לראות שיש כמה משתנים שרמת המובהקות שלהם גדולה מ 0.05 ולכן נסיר אותם מהרגרסיה ונריץ אותה שוב בלעדיהם:
results_logit = smf.logit('aircon ~ price+stories+gasheat ', data=houses).fit()
print(results_logit.summary())
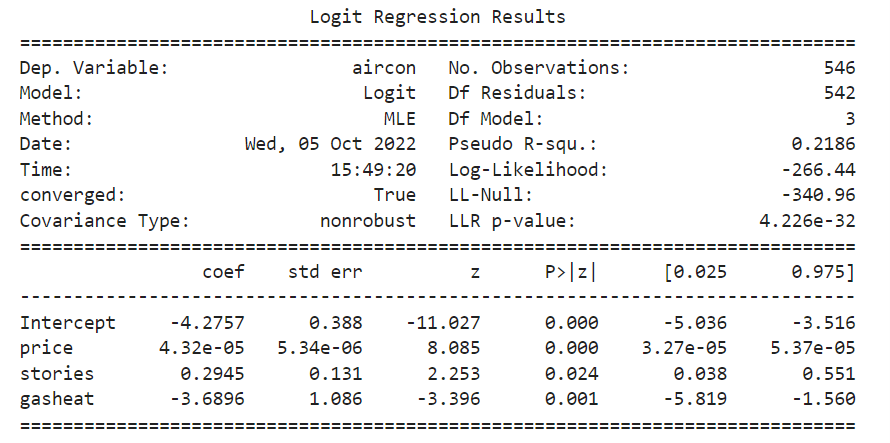
עכשיו כאשר כל המשתנים מובהקים ננסה להסביר מה ההשפעה שלהם על המשתנה התלוי – הימצאות מזגן בדירה.
בחינת ההשפעה של משתנים בלתי תלויים על המשתנה התלוי ברגרסיה לוגיסטית
כדי לחשב את ההשפעות של כל משתנה בלתי תלוי במודל יש להריץ פונקציית exponent על המקדמים (coef) שקיבלנו ברגרסיה. לכן נריץ את הפקודה:
print(np.exp(results_logit.params))
ונקבל את התוצאות הבאות:
Intercept 0.01
price 1.00
stories 1.34
gasheat 0.02
פירוש התוצאות
לפי תוצאות הרגרסיה כל קומה בדירה מעלה את הסבירות שבדירה יהיה מזגן פי 1.34 (odds ratio). בממוצע ובתנאי שכל שאר המשתנים נשארים אותו הדבר, המחיר אינו משפיע על הסיכוי לכך שיהיה מזגן בדירה ולדירות המחוממות בגז הסבירות למצוא בהן דירה עם מזגן יורדת פי 0.02.
הערות:
- כמו כל מודל סטטיסטי גם לרגרסיה לוגיסטית יש לעשות בדיקות תיקוף.
- כמו כן, במאמר לא התייחסתי לנושא של הנחות היסוד שיש לבדוק לפני שמריצים רגרסיה לוגיסטית.
לחברות המעוניינות בשירותי פרילנס או סדנאות של אנליסט, ניתן לפנות אליי [email protected]
לחלקים הקודמים של המדריך
מדריך ניתוח נתונים בשפת פייתון – חלק א.
מדריך ניתוח נתונים בשפת פייתון – חלק ב.
מדריך להתקנת פייתון בחינם.
מאמרים נוספים בנושא
**** לפודקאסט של הבלוג לחצו כאן ****

